ACCT 101: Bonds
Session 8
Dr. Richard M. Crowley
Frontmatter
Quiz 2
- Covers everything since Quiz 1
- Inventory
- PP&E
- Intangibles
- Liabilities
- Bonds
- For calculations, the level of rounding will be specified
- Same format as quiz 1
- Practice quiz and additional practice are on eLearn
Learning objectives
Liabilities (Chapter 9)
- Account for bonds at par
- Account for bonds not at par
- Account for bond buybacks
Bonds
What is a bond?
- An interest bearing note payable
- Issued by a company in a manner similar to stock
- Often to investors (like stock)
- Trades on an exchange daily (like stock)
- Does not offer ownership
- For the simpler bonds we’ll cover in this course
- Usually due in 5 or 10 years, frequently longer
- Interest is usually paid every 6 months

Types of bonds
- Backing
- Secured bonds: Backed by assets such as real estate (mortgage bonds) or other assets (collateral trust bonds)
- Unsecured bonds: No asset backing; also called debentures
- Principal Payments
- Term Bonds: Mature on a single date
- Serial bonds: Pay off principal in installments
- Other features
- Convertible bonds: Bonds that can be converted into common stock at the creditor’s request
- Callable bonds: Bonds that can be paid early at a stated amount prior to maturity at the debtor’s request
You only need to price unsecured term bonds in this course
Bond characteristics
- From the bond holder’s perspective
- Higher precedence than stock during bankruptcy
- No voting rights
- No ownership
- From the bond issuer’s perspective
- Interest payments are tax deductible
- Guaranteed cash outflows
- Raises funds without giving up ownership
Life of a bond
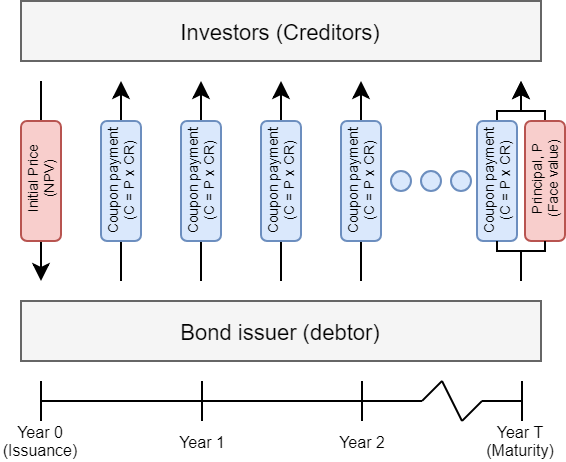
Bond terms
- Term: length of time of the bond
- Maturity date: when the bond is due
- Par value: The amount the bond will pay at maturity
- Aka: principal amount, maturity value, face value
- Coupon rate: Yearly % of interest paid
- Aka: Stated interest rate, nominal rate
- Yield: Yearly percent return if you purchase the bond today
- This was our discount rate last week
- Aka: Market interest rate, effective interest rate
- Price: % of par value you need to pay to purchase
- \(100 \Rightarrow\) Full price, “At par”
- \(<100 \Rightarrow\) Discount
- \(>100 \Rightarrow\) Premium
Bond quote terms
- CUSIP: Unique identifier given to the bond
- Name: Name given to the bond
- Day count: 30/360 or actual
- 30/360: Assumes 30 days per month, 360 days per year
- Most common day count for bonds
- Easier to calculate
- Actual: Count the number of days
- 30/360: Assumes 30 days per month, 360 days per year
Bond quotes available at Morningstar
How to do day counts
- Actual/Actual day count:
- Use the actual number of days divided by the number of days in the year (365 or 366)
- 30/360 day count:
- Full months have 30 days each
- Full years have 360 days
- If the starting date is the last day of the month, call it the 30th
- If the adjusted starting date is the 30th, then if the ending date is the last day of a month, call it the 30th as well
- If not, the 31st becomes the 1st of the next month
- If not, the 28th or 29th (February) stays where it is
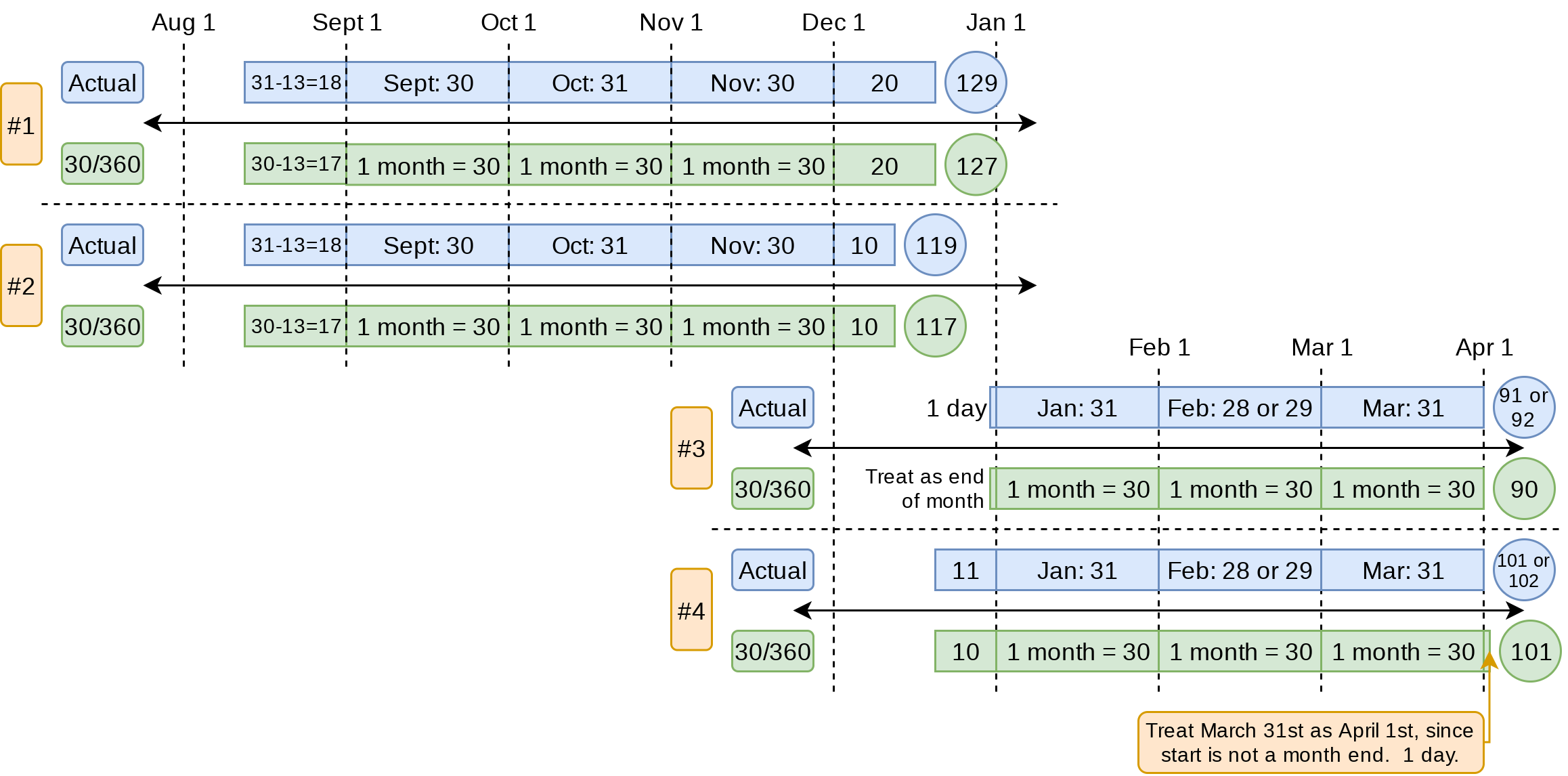
Example: Between June 20th and August 25th, there are actually 66 days. Using 30/360, we say there are 65 days
How to do day counts

Day counts, 30/360
- How many days are there between August 13th and December 20th?
- How many days are there between August 13th and December 10th?
- How many days are there between December 30th and March 31st?
- How many days are there between December 20th and March 31st?
Day counts, 30/360
Valuing bonds
Recap of NPV
- We had 2 formulas last week that will help us calculate bond values
- Single cash flow in the future: \(NPV = \frac{CF}{(1+r)^T}\)
- Repeated cash flow (annuity): \(NPV = \frac{CF}{r} \cdot \left[1-\frac{1}{(1+r)^T}\right]\)
- From an investor’s perspective, a bond is:
- An initial payment
- An annuity received every 6 months
- Annuity: Receiving the same cash flow every period for a set number of periods
- A final cash flow
- Investors pay the NPV of a bond when discounting by the yield
Let’s value a bond!
- The bond: MSFT.GG
- Microsoft issued on September 27, 2010
- 10 year bond
- \(3.10\%\) yield when it was issued
- \(3.00\%\) coupon rate
- Semiannual coupon payments (interest payments)
- 30/360
- $1B par value, in total
- One trick needed:
- Since this (and most other) bonds pay their interest semiannually, we need to calculate using half-years
Using our NPV formulas
How much would investors pay for the bond?
- Principal, \(P\), is $1B
- Annuity cash flow = \(3.00\%\) of principal per year, paid in 2 payments
- \(3\% \times \$1B = \$30M\) per year, so \(CF=\$15M\) semiannually
- Discount rate = yield = \(3.10\%\), \(r=\frac{3.10\%}{2}=1.55\%\) semiannually
- Number of semiannual periods, \(T=20\)
Using our NPV formulas: Annuity
- \(P=\$1B\), \(CF=\$15M\), \(r=1.55\%\), \(T=20\)
Annuity portion
\[\begin{align*} Annuity\ NPV&=\frac{CF}{r} \cdot \left[1-\frac{1}{(1+r)^{T}}\right] \\ &=\frac{15M}{0.0155} \cdot \left[1-\frac{1}{(1+0.0155)^{20}}\right] \\ &\approx \$256M \end{align*}\]
Using our NPV formulas: Principal
- \(P=\$1B\), \(CF=\$15M\), \(r=1.55\%\), \(T=20\)
Final cash flow (principal)
\[\begin{align*} Principal\ NPV&=\frac{P}{(1+r)^T} \\ &= \frac{\$1B}{(1+0.0155)^{20}} \\ &\approx \$735M \end{align*}\]
Using our NPV formulas: Principal
- \(P=\$1B\), \(CF=\$15M\), \(r=1.55\%\), \(T=20\)
Bond price, i.e., bond NPV
\[\begin{align*} NPV&= Annuity\ NPV + Principal\ NPV \\ &= \$256M + \$735M \\ &= \$991M \end{align*}\]
- This means that investors paid $991M for the bond issue when it was issued.
Note: If you solve this more precisely, you will get an answer $.01M off from Morningstar’s price, as the bond was actually a 10 year and 3 day issue. We will ignore those 3 days. We won’t deal with these fractional years for bond pricing.
Simplifying our equation
- We can bring everything together into 1 equation:
\[\begin{equation*} Price = \frac{CF}{r} \cdot \left[1-\frac{1}{(1+r)^T}\right] + \frac{P}{(1+r)^T} \end{equation*}\]
- Variables:
- \(P\): Principal amount, aka the par value
- \(i\): Coupon rate
- \(y\): Yield
- \(Y\): Length of bond, in years
- \(n\): Number of payments per year
- Then:
- \(CF=\frac{P\times i}{n}\): Cash flow per coupon
- \(T=Y\times n\): Number of payments
- \(r=y/n\): Discount rate
Applying the equation to our bond
\[\begin{equation*} Price = \frac{CF}{r} \cdot \left[1-\frac{1}{(1+r)^T}\right] + \frac{P}{(1+r)^T} \end{equation*}\]
- Given:
- \(P=\$1B,\quad i=3\%,\quad y=3.10\%,\quad Y=10,\quad n=2\)
- Calculate:
- \(CF=\frac{p\times i}{n} = \frac{\$1B \times 3\%}{2}=\$15M\)
- \(T=Y\times n=10\times 2 = 20\)
- \(r=y/n = 3.10\%/2 = 1.55\%\)
\[\begin{align*} Price &= \frac{\$15M}{0.0155} \cdot \left[1-\frac{1}{(1+0.0155)^{20}}\right] + \frac{\$1B}{(1+0.0155)^{20}} \\ &\approx \$991M \end{align*}\]
What about the table method?
- The table method is allowed on the final exam, and annuity and NPV tables will be provided
- Table equation: \(Price=CF \times Annuity\_factor + P\times NPV\_factor\)
- \(Annuity\_factor\) comes from the cell in the annuity table corresponding to \(T\) periods and \(r\) discount rate
- \(NPV\_factor\) comes from the cell in the NPV table corresponding to \(T\) periods and \(r\) discount rate
The equation method is more accurate, works for any \(r\) and \(T\), and can also be used in your other classes
Practice
- Bond: McDonald’s MCD4248397
- Principal of $700M
- Coupon rate of 2.2%
- Yield of 2.24%
- 5 year bond
- Semiannual coupon payments
What is the price?
Solution
- \(P = \$700M\)
- \(CF = \$700M \times 2.2\%/2\ per\ year=\$7.7M\)
- \(T = 5\ years \times 2\ per\ year = 10\text{ half-years}\)
- \(r = 2.24\%/2\ per\ year = 1.12\%\)
\[ \begin{align*} Price &= \frac{CF}{r} \cdot \left[1-\frac{1}{(1+r)^T}\right] + \frac{P}{(1+r)^T} \\ &= \frac{\$7.7M}{0.0112} \cdot \left[1-\frac{1}{(1+0.0112)^{10}}\right] + \frac{\$700M}{(1+0.0112)^{10}} \\ &= \$698.68M \end{align*} \]
Accounting for bonds: Par
Accounting for bonds
- We need to know:
- Principal
- Price (we can solve for this if not given)
- Yield
- Coupon amount (or rate)
- Coupon payments per year
- Count basis (30/360 usually)
- Types of bonds:
- Bond at par: Coupon rate = yield \(\Leftrightarrow\) price = par value
- Discount bond: Coupon rate < yield \(\Leftrightarrow\) price < par value
- Premium bond: Coupon rate > yield \(\Leftrightarrow\) price > par value
- Steps
- Account for bond issuance
- Account for coupon payments
- Account for accrued interest expense at year end
- In the final period, pay back the principal
Bonds at par
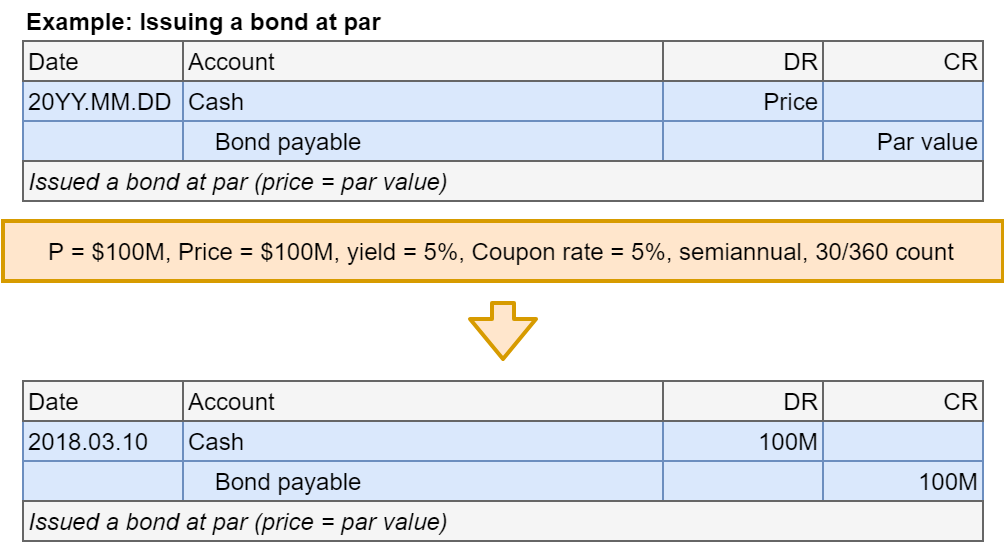
- Example bond for these slides:
- Principal = $100M
- Price = $100M
- Yield = 5%
- Coupon rate = 5%
- Semiannual coupon payments (every 6 months)
- Count basis: 30/360
- Assume it’s a 10 year bond issued on March 10th, 2018
- Assume the firm issuing the bond uses a Dec 31 year end
Bonds at par: Issuance
- If a bond is at par value, the accounting is the same structure as a note payable
- Step 1: Account for bond issuance
Bonds at par: Coupon payment
- Step 2: Account for coupon payments
- Interest expense
- Cash payment is the coupon

Bonds at par: Adjusting entry
- Step 3: Account for accrued interest expense at year end
- The accrued interest is based on the number of days
- We’ll use 30/360 day counts unless otherwise stated
- Interest owed will be \(CF \times \frac{days}{180}\)
- The accrued interest is based on the number of days

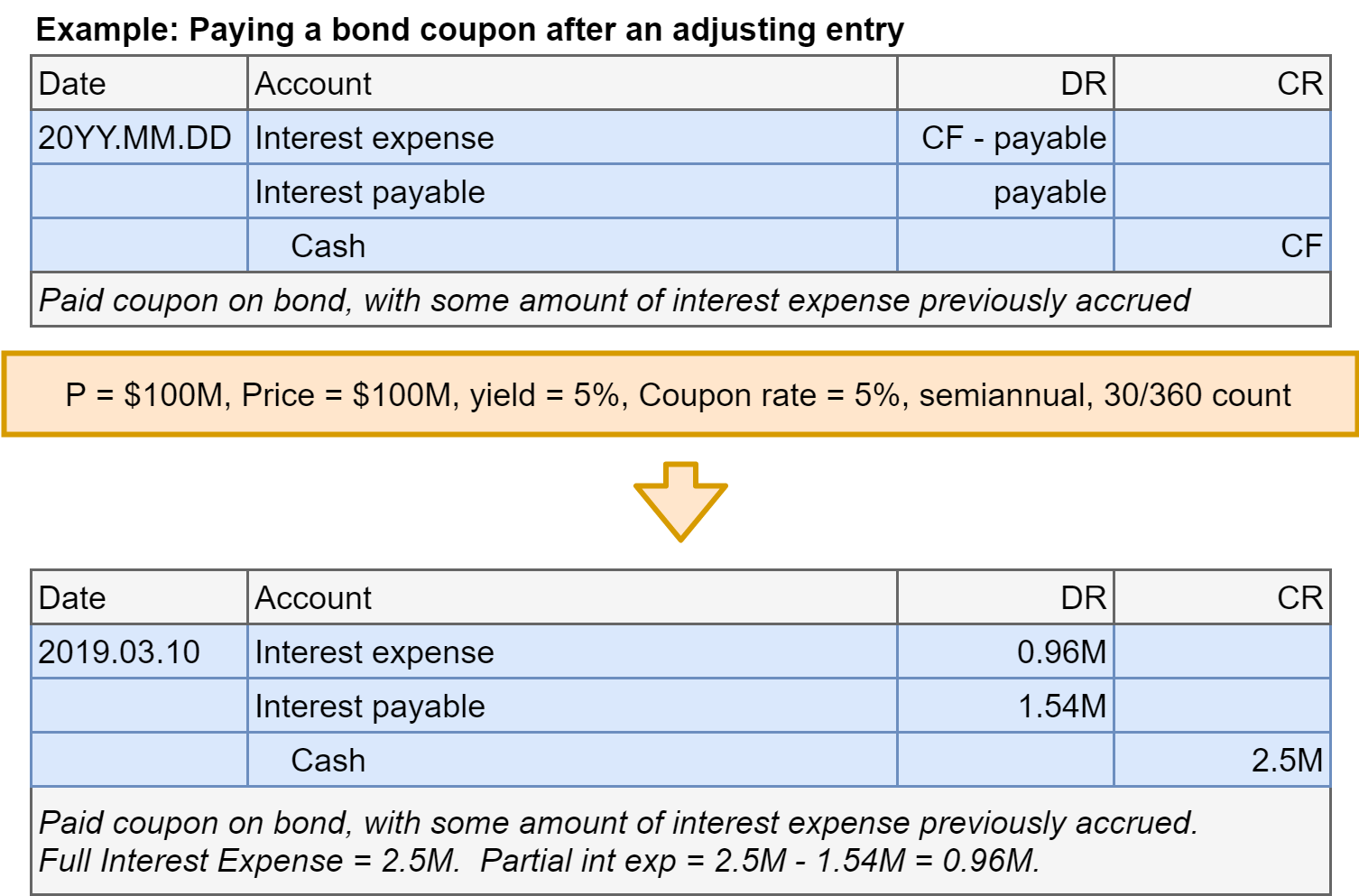
Bonds at par: Coupon after adjusting
- Step 2 revisited: Account for coupon payments
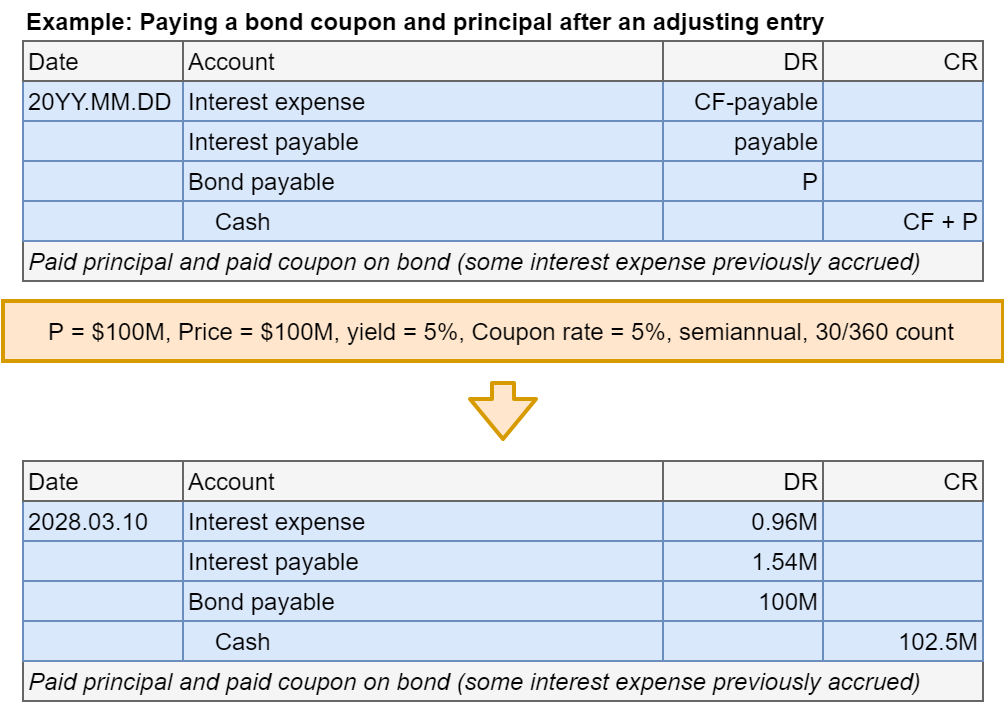
Bonds at par: Final payment
- Step 4: In the final period, pay back the principal (and a coupon)
- Since interest expense is the same every period for bonds at par, we can figure this out
Practice: Bonds at par
- Bond: Ford’s F.GD
- Principal: $366.53M
- Yield: 9.3%
- Coupon rate: 9.3%
- Semiannual coupons
- 30/360
- Issued on March 1, 1998
- 32 year bond
- Note: Ford’s fiscal year ends on December 31
Determine Ford’s journal entries for the bond for issuance, the first coupon, the adjusting entry, and the second coupon
Accounting for bonds: Discount
Discount bonds
- Trading at a price below par!
- Equivalent to having a coupon rate lower than yield
- Example bond for these slides:
- Principal = $100M
- Price = $92.56M
- Yield = 6%
- Coupon rate = 5%
- Semiannual coupon payments (every 6 months)
- Count basis: 30/360
- Assume it’s a 10 year bond issued on March 10th, 2018
- Assume the firm issuing the bond uses a Dec 31 year end
Effective interest method
- Recall:
- Bond payable amount is the par value
- Cash amount is the price
- Since these aren’t equal, our very first entry won’t balance!
We’ll use the Effective Interest Method to fix this
- Record a contra-liability to our bond payable to reflect the difference
- Account name is Discount on bonds payable
- Over time, we remove the discount by recording extra interest expense each period
- Define Carrying value to be \(Payable-Discount\)
Interest expense will be \(Carrying\ value\times yield/n\)
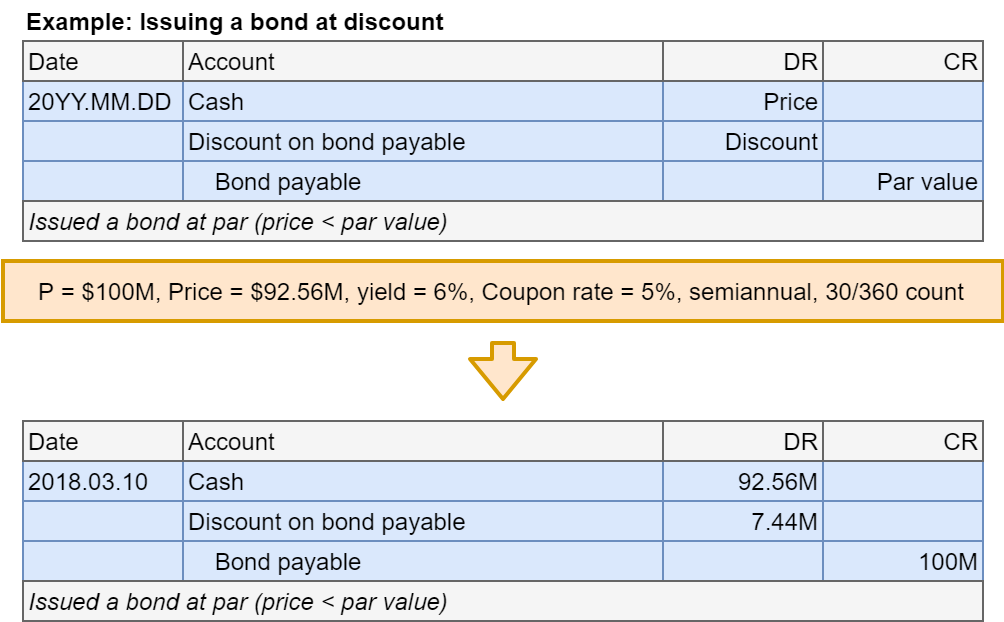
Bonds at discount: Issuance
- Step 1: Account for bond issuance
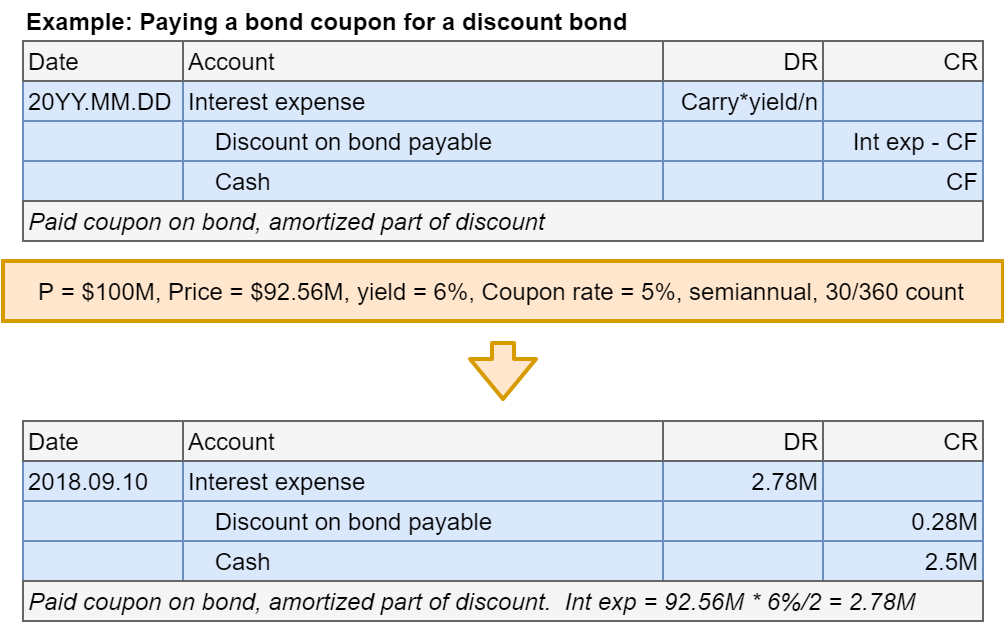
Bonds at discount: Coupon payment
- Step 2: Account for coupon payments
- Need to use the effective interest method!
Bonds at discount: Adjusting entry
- Step 3: Account for accrued interest expense at year end
- Interest owed and interest expense will be multiplied by \(\frac{days}{180}\)
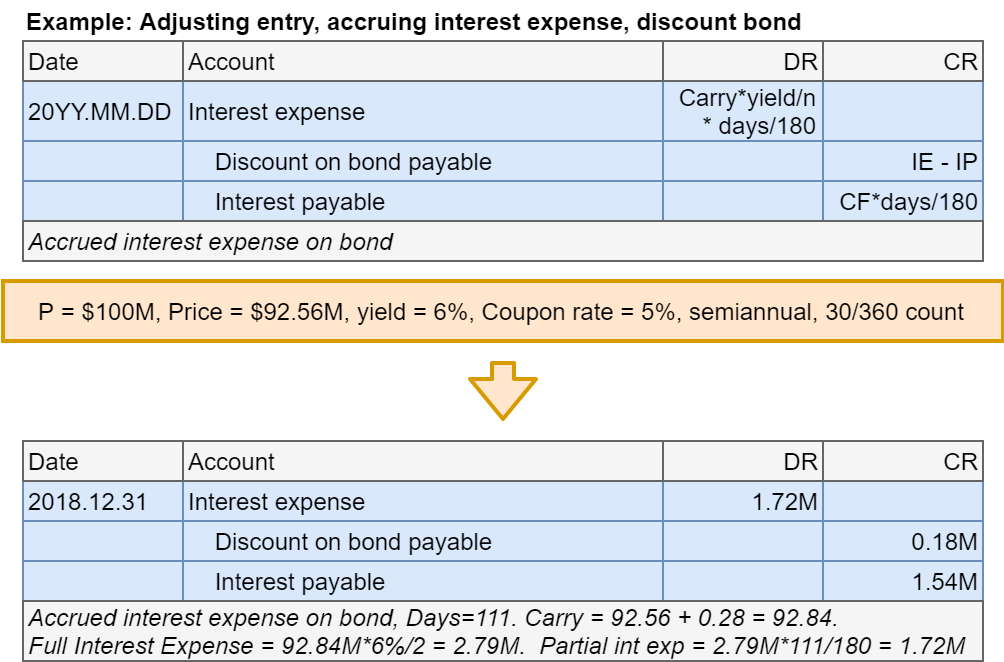
Bonds at discount: Coupon after adjusting
- Step 2 revisited: Account for coupon payments
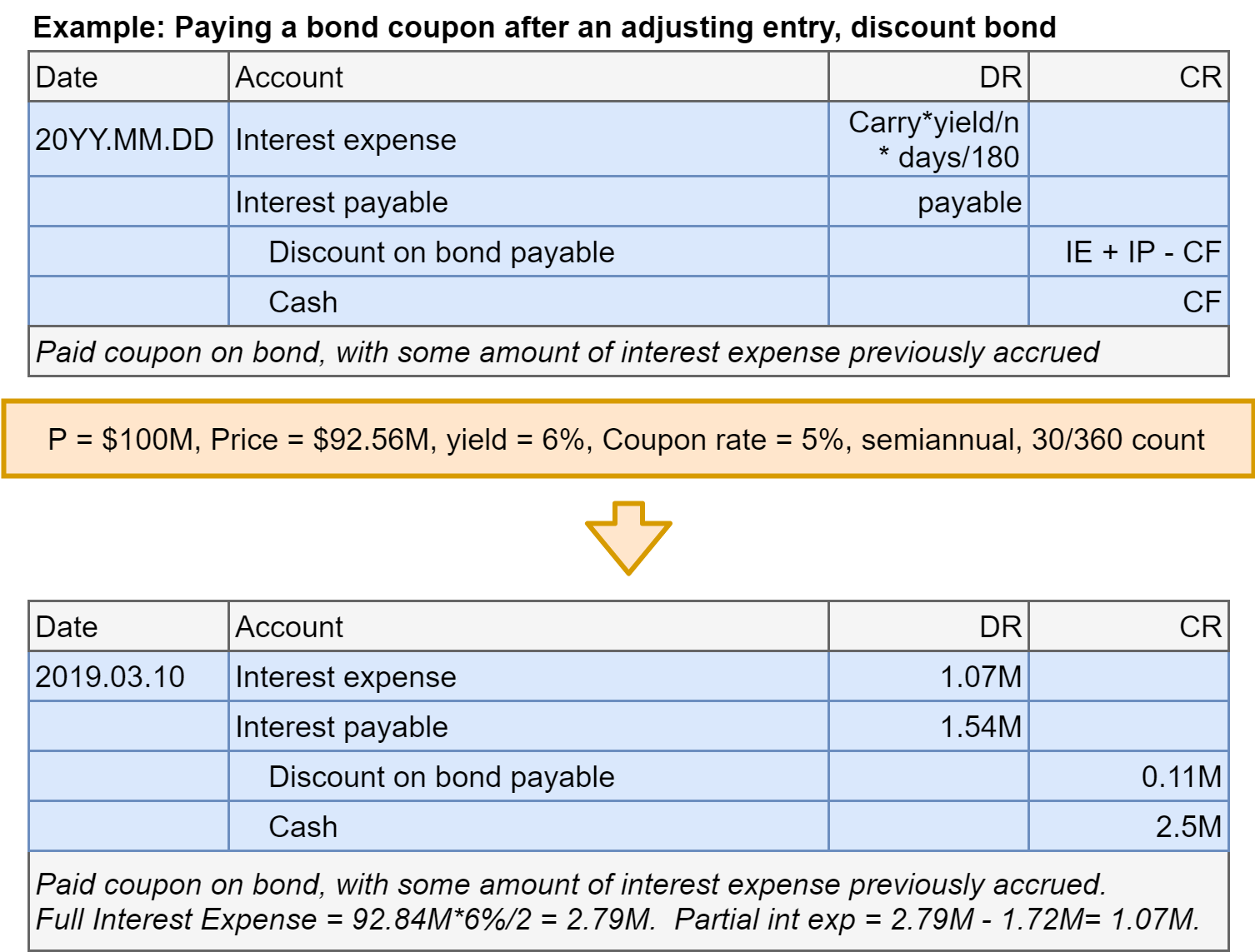
Bonds at discount: Final payment
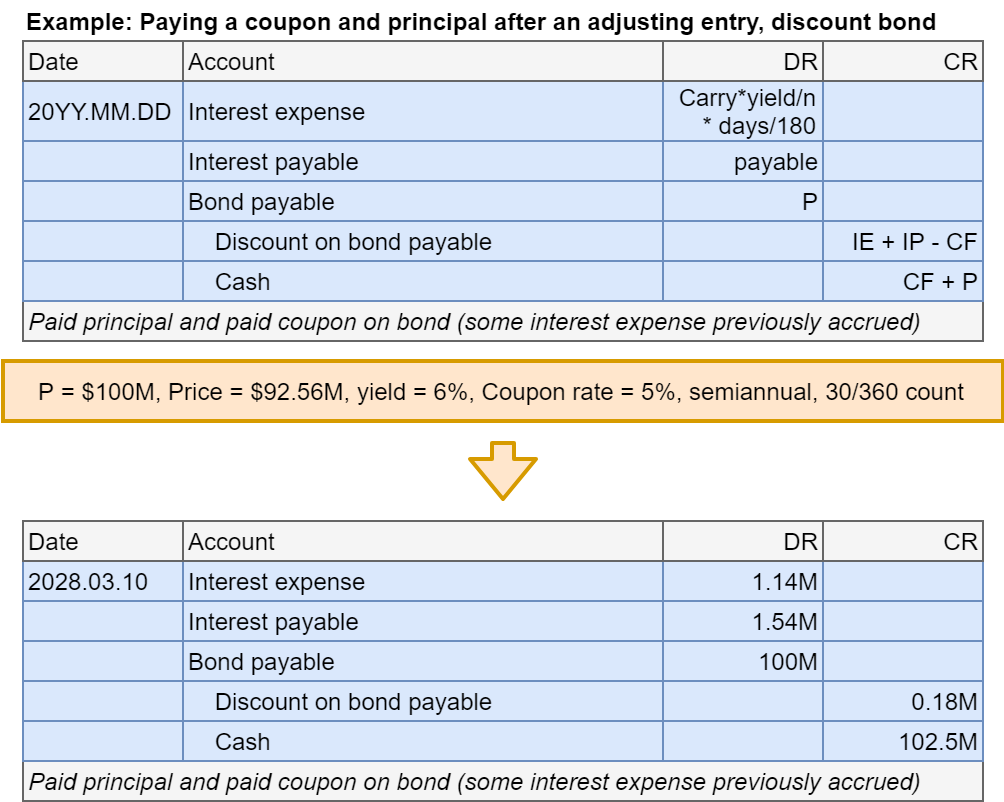
- Step 4: In the final period, pay back the principal (and a coupon)
- You won’t be asked to figure this out without extra information
Accounting for bonds: Premium
Premium bonds
- Trading at a price above par!
- Equivalent to having a coupon rate higher than yield
- Example bond for these slides:
- Principal = $100M
- Price = $108.18M
- Yield = 4%
- Coupon rate = 5%
- Semiannual coupon payments (every 6 months)
- Count basis: 30/360
- Assume it’s a 10 year bond issued on March 10th, 2018
- Assume the firm issuing the bond uses a Dec 31 year end
Effective interest method
- Recall:
- Bond payable amount is the par value
- Cash amount is the price
- Since these aren’t equal, our very first entry won’t balance!
We’ll use the Effective Interest Method to fix this
- Record a liability along with our bond payable to reflect the difference
- Account name is Premium on bonds payable
- Over time, we remove the premium by recording lower interest expense each period
- Define Carrying value to be \(Payable+Premium\)
Interest expense will be \(Carrying\ value\times yield/n\)
Bonds at premium: Issuance
- Step 1: Account for bond issuance
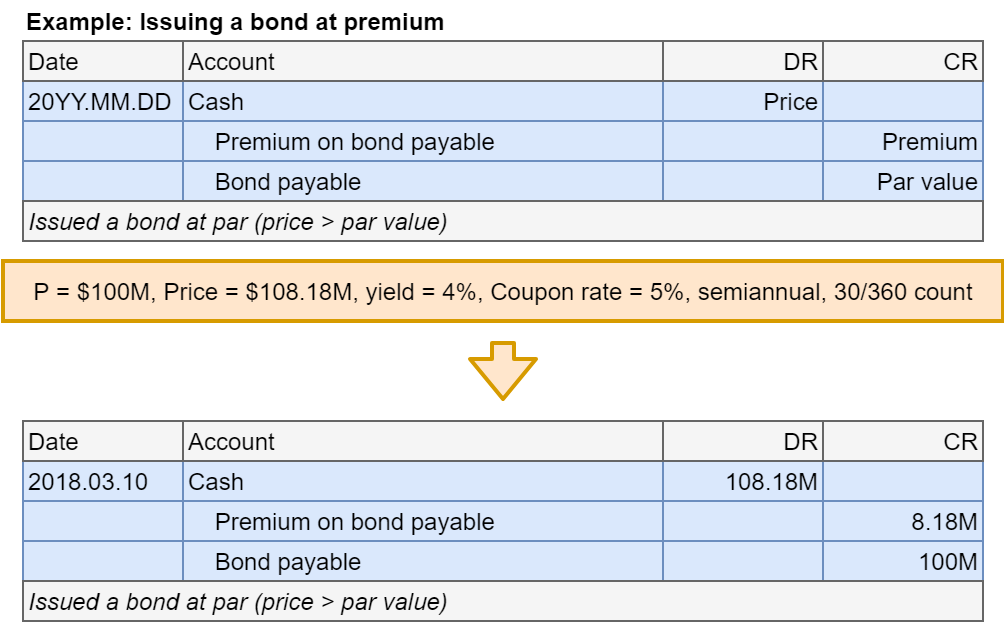
Bonds at premium: Coupon payment
- Step 2: Account for coupon payments
- Need to use the effective interest method!
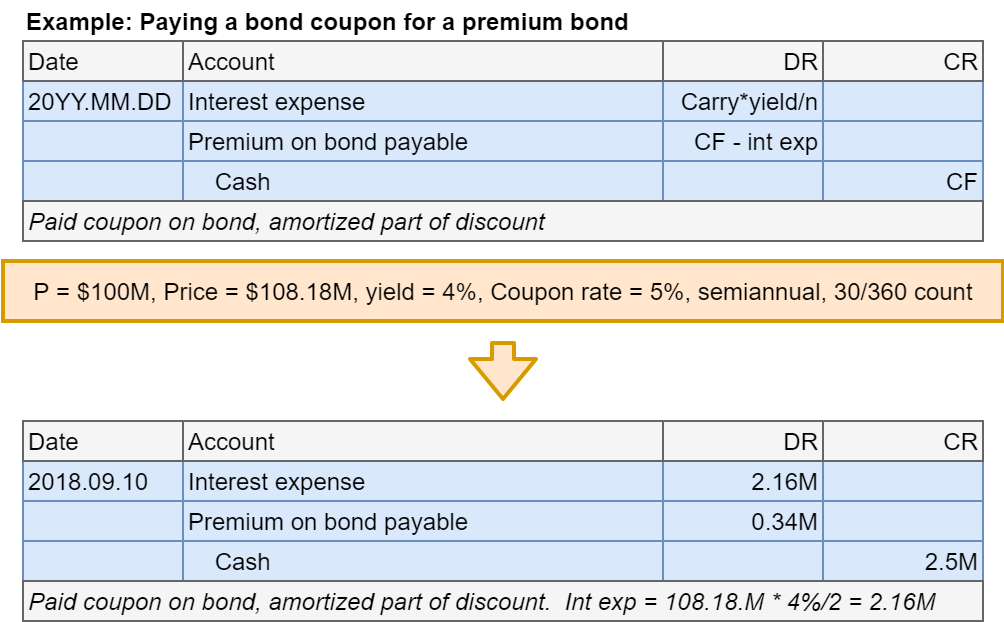
Bonds at premium: Adjusting entry
- Step 3: Account for accrued interest expense at year end
- Interest owed and interest expense will be multiplied by \(\frac{days}{180}\)
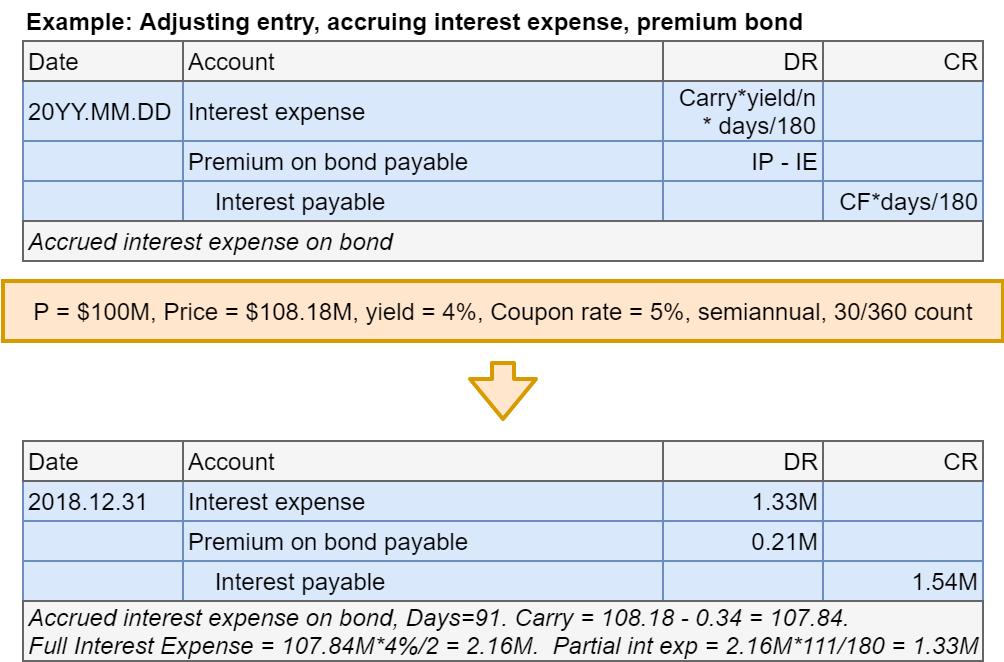
Bonds at premium: Coupon after adjusting
- Step 2 revisited: Account for coupon payments
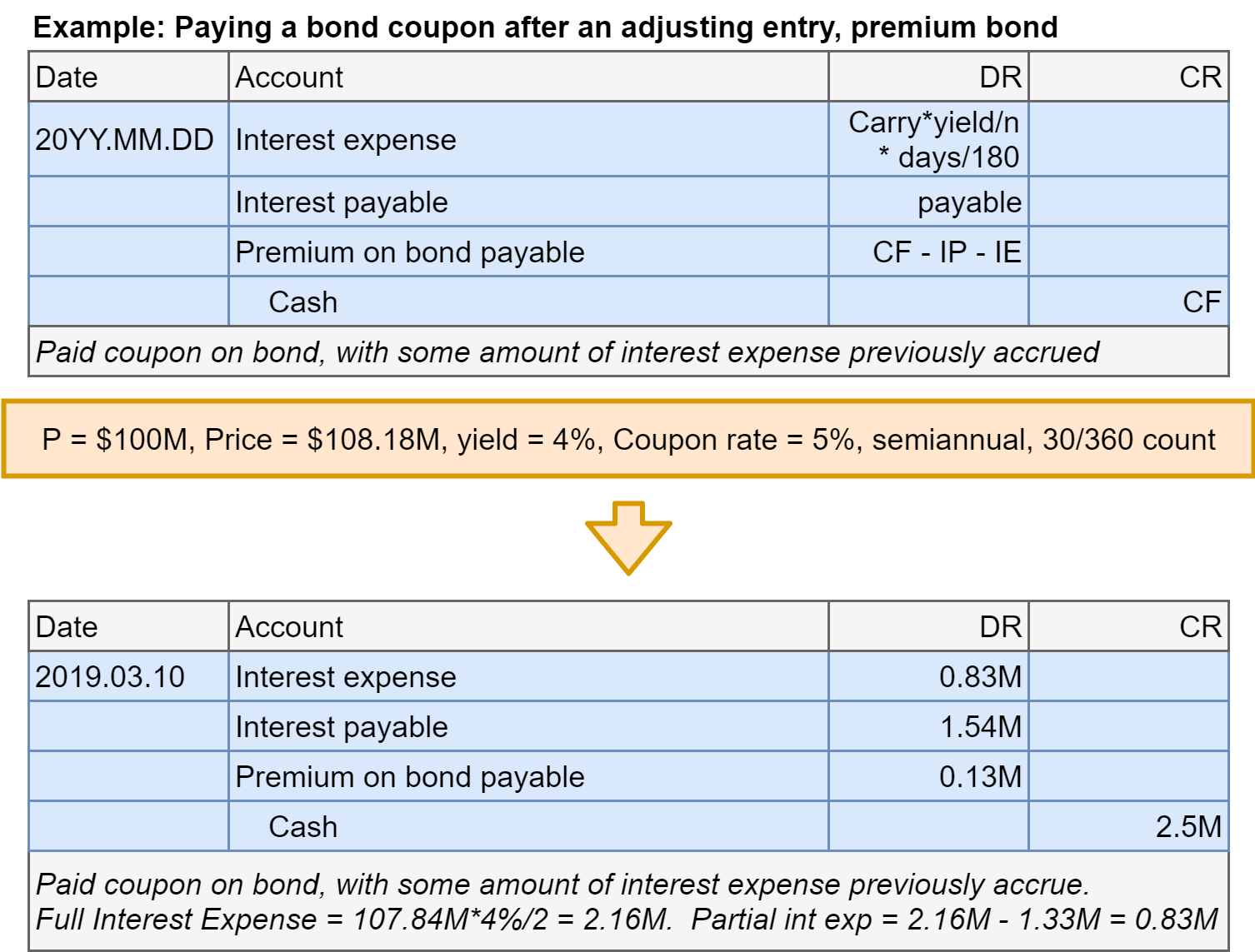
Bonds at premium: Final payment
- Step 4: In the final period, pay back the principal (and a coupon)
- You won’t be asked to figure this out without extra information
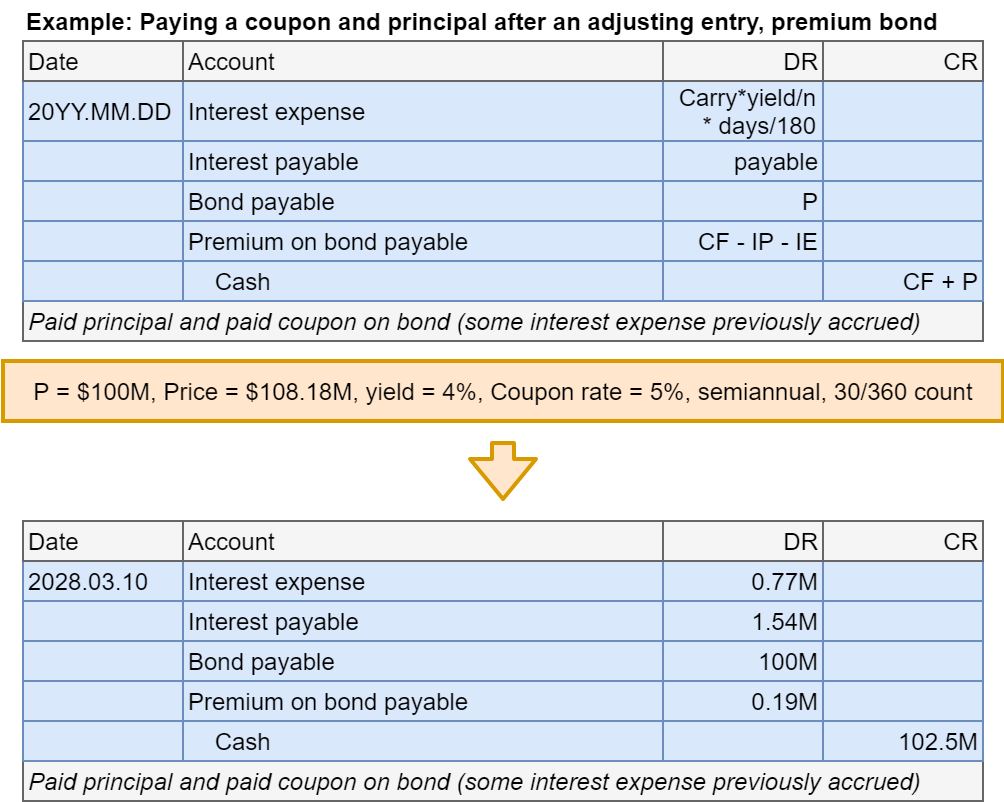
Bonds not at par
What’s actually going on here?
- The effective interest method distributes the discount or premium over the life of the bond
- The discount or premium hits 0 just as the last coupon is paid
- Discounts lead to higher expenses each year
- We treat the shortfall in cash for a discount bond as a large amount of interest expense, and amortize it over the life of the bond
- Premiums lead to lower expenses each year
- We treat the excess cash for a premium bond as free money that will cancel out some of our interest payments, and thus we amortize it over the life of the bond
Visualizing Carrying value
Interest Expense
Practice: Bonds not at par
For each of the following bonds, calculate the price and determine Ford’s journal entries for the bond for issuance, and the next 3 journal entries (1 adjusting and 2 coupon payments). Ford’s fiscal year end is December 31st.
- Bond: Ford’s F.GY (Discount)
- Principal: $1,800M
- Yield: 7.53%
- Coupon rate: 7.45%
- Semiannual coupons
- 30/360
- Issued on July 16, 1999
- 32 year bond
- Bond: Ford’s F.GI (Premium)
- Principal: $300M
- Yield: 9.04%
- Coupon rate: 9.950%
- Semiannual coupons
- 30/360
- Issued on February 15, 1992
- 40 year bond
Bond retirement
Bond retirement
- Firms can retire a bond in two ways:
- Work with creditors to establish a price to pay to end the bond.
- Buy back bonds on the market.
- To retire a bond:
- Record any accrued interest expense
- Debit out the bond payable account and any interest payable
- Close out any premium or discount account
- Credit the amount of cash paid to retire the bond
- Record the difference to a gain on bond retirement if credit balance, or to a loss on bond retirement if debit balance
Bond retirement example: Bond at par
Suppose our example bond at par was retired after 1.25 years, on 2019.06.10, for par plus accrued interest.
- Par: $100M, Coupon rate: 5%, Yield: 5%
- Carrying value on 2019.03.10: $100M
- Accrued interest (to pay): \(\$100M \times \frac{5\%}{2} \times \frac{90}{180}=\$1.25M\)
- Accrued interest expense: \(\$100M \times \frac{5\%}{2} \times \frac{90}{180} = \$1.25M\)

Bond retirement example: Discount bond
Suppose our example discount bond was retired after 1.25 years, on 2019.06.10, for par plus accrued interest.
- Par: $100M, Coupon rate: 5%, Yield: 6%
- Carrying value on 2019.03.10: $93.12M (discount: $6.88M)
- Accrued interest (to pay): \(\$100M \times \frac{5\%}{2} \times \frac{90}{180}=\$1.25M\)
- Accrued interest expense: \(\$93.12M \times \frac{6\%}{2} \times \frac{90}{180} = \$1.40M\)

Bond retirement example: Premium bond
Suppose our example premium bond was retired after 1.25 years, on 2019.06.10, for par plus accrued interest.
- Par: $100M, Coupon rate: 5%, Yield: 4%
- Carrying value on 2019.03.10: $107.50M (premium: $7.50M)
- Accrued interest (to pay): \(\$100M \times \frac{5\%}{2} \times \frac{90}{180}=\$1.25M\)
- Accrued interest expense: \(\$107.50M \times \frac{4\%}{2} \times \frac{90}{180} = \$1.07M\)

End matter
For next week
- Quiz 2
- Reading
- Chapter 11 (Cash flows)
- Homework 4: Bonds
- Graded based on effort!
- Extra practice available
- Bonds eLearn quiz
- Quiz 2 practice exam
- Quiz 2 additional practice
- Quiz 2 book problems
- Survey on the class session at rmc.link/101survey8
NOTES
The 30/360 calculation slide part on End of month is ambiguous. Replace with a flow chart or something else clearer
How about revamping the discount/premium bonds to be taught using amortization tables? Might be more straightforward…
- Nope – the equation works well