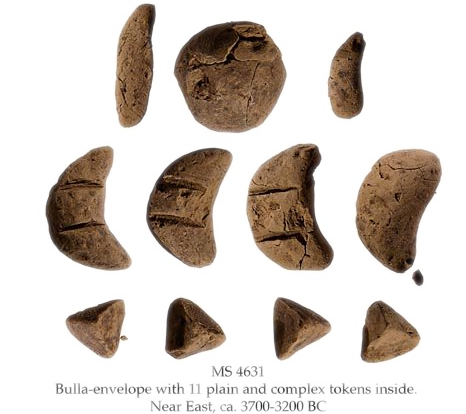
History and Bookkeeping
Theory Session #1
Dr. Richard M. Crowley
rcrowley@smu.edu.sg
http://rmc.link/
Accounting History
History: Before double entry
- 8500 BCE: Shaped clay tokens represent commodities
- 200 BCE: Arabic numerals (except 0)
- 600 CE: 0 developed
- 800 CE: 10-digit numerals spread throughout Europe

*Note: This slide is based on a history lecture by Dr. Pierre Liang at Carnegie Mellon from October 2017
History: Double entry
- 1400s CE: First evidence of double entry bookkeeping in Italy
- 1494 CE Italian monk and scholar Luca Pacioli publishes first text on double entry bookkeeping


*Note: This slide is based on a history lecture by Dr. Pierre Liang at Carnegie Mellon from October 2017
History: Journal entries




Images from Littleton 1928 TAR.
History: Journal entry evolution

Shakespeare likely did this sort of work for the British Navy! (Source: Reynolds 1974 JAR)
A note on journal entries
- Journal entries \(\neq\) Double entry
- You can create a single entry journal entry
- Or a triple entry!
- You can create a single entry journal entry
- Journal entries are not needed for double entry to function
- Littleton (1928) makes this point, arguing that ledgers are sufficient, so long as adjustments to ledgers follow the principles of double entry
Modern history of bookkeeping
- 1845 CE: Business corporation law passed in England
- 1887 CE: AAPA founded (Predecessor to AICPA)
- American Association of Public Accountants
- 1904 CE: ACCA founded in London
- 1934 CE: Securities Exchange Act establishes the SEC, mandates audits
- 1940 CE: Paton and Little monograph published
- A serious discussion of accounting standards, rather than principles
- 1973 CE: FASB replaces the APB
*Note: This slide is based on a history lecture by Dr. Pierre Liang at Carnegie Mellon from October 2017
History: Impact
The Principles of Book-keeping by Double Entry constitute a theory which is mathematically by no means uninteresting: it is in fact like Euclid’s theory of ratios an absolutely perfect one, and it is only its extreme simplicity which prevents it from being as interesting as it would otherwise be.
– Arthur Cayley, FRS, The Principles of Book-keeping by Double Entry, 1894.
Bookkeeping has become a real technology instead of a simple clerical routine, and in addition there has grown up a profession of accounting which reaches quite beyond bookkeeping.
– A. C. Littleton, The Evolution of the Journal Entry, 1928.
Why do we care about bookkeeping?
- Without bookkeeping, what would be left of accounting?
- Why does so little research focus on bookkeeping?
- What could we do if we had access to companies’ bookkeeping records?
- What does our lack of such records mean for our discipline?
Why do we care about bookkeeping?
- From Hatfield (1924), bookkeeping is respectable in at least three ways:
- Lineage
- Respectability of those that studied accounting
- Services provided to society
The Lineage of bookkeeping
- Double entry, as we generally think of it, was formalized in a chapter of Luca Pacioli’s Summa, as a section titled De Computis et Scripturis
- Pacioli was:
- A well respected Italian mathemetician
- A coauthor of Leonardo Da Vinci
- Summa stood as the authority on bookkeeping for >100 years
- Pacioli was:
“Let those who vaunt the superior merits of other disciplines remember that this first presentation made by Paciolo was not crude and incorrect but contains the essentials of bookkeeping as we know it today, despite the fact that it was written at a time when chemistry partook of the vagaries of alchemy, biology was a weird collection of errors, and medicine had more in common with the medicine man than it has even today.”
Those that studied accounting historically
- Luca Pacioli: Well respected mathemetician
- Henricus Grammateus: Mathematician, first to publish on bookkeeping in German
- Jerome Cardan: Polymath
- “astrologer, physician, scientist, mathemetician, professor of medicine”
- Before 1800, writers on bookkeeping included authorities on:
- Algebra, navigation, optics, foreign exchange, author of the Code Savary, astronomy, grammar, gunpowder, history
- Four members of the Royal Society
- After 1800:
- Augustus De Morgan: De Morgan’s laws (e.g., \(\overline{A\cup B} = \overline{A} \cap \overline{B}\))
- Arthur Cayley: Renowned mathemetician
Service to society
- That bookkeeping exists is not by chance
- “Bookkeeping arose as a direct result of the establishment of partnerships on a large scale, a feature of expanding commerce” (Sieiveking, in Hatfield 1924)
- The expansion of trusts (precursor to corporations in present society) led to an explosion in demand for bookkeeping
- The “billion dollar corporation”
Expansion of bookkeeping?
- What about present society, with the “trillion dollar corporation?”
If the substitution of a small partnership for the individual trader called for improvement in bookkeeping methods, how much more was improvement needed when the partnership was displaced by the corporation with its owners numbered by the tens of thousands?
The use of fixed capital on a large scale increases incalculably the difficulty of determining the profits earned in any given year.
Where are we at?
In 1924
- Hatfield (1924) argues that there were two primary areas of progress:
- Methods of handling large quantities of calculations
- An “attempt to ascertain the exact cost of producing objects or parts of objects”
In 2007
- Fellingham (2007), “Is Accounting an Academic Discipline?”
- Disconnect between teaching and research
- We emphasize standards instead of our “best ideas” – emphasize the vocational
- Heavy focus on clinical faculty
- Revelation of DBA programs
- Focus on rankings rather than academics in teaching
- Focus on revenue generation at universities
- Progress on the “science of information”
- Accounting as an information science?
- Disconnect between teaching and research
Also In 2007
- Demski (2007), “Is Accounting an Academic Discipline?”
- No, “the vocational focus is overwhelming”
- “Innovation is close to nonexistent”
- Something like the ratcheting effect at work
- Laments the lack of information science in our curriculum
- “Double entry, in fact, is a primitive error-detecting code”
Demski’s characterization of accounting research
“Accounting per se has disappeared from our activities. Likelihood structures or random variables routinely substitute for accounting structure. Simple models of accruals, as opposed to sophisticated, economic-based structural models, based on accounting structure and economic fundamentals, are routinely employed in our research and teaching. And most telling, choices in accounting measurements are routinely ignored, such as the choice to nudge EPS or to forecast at a specific time and with a specific amount. Indeed, virtually no issue in accounting would exist were it not for management’s choice behavior, though this is treated as largely second order in the vast bulk of our teaching and research.”
How to get back to our academic roots?
- “[Accounting] could and should […] be an academic discipline”
- What is missing? Passion
- “Our responsibility is not to prosper in this culture or to do well; it is to do good.”
- “At this point, the only path I see is mutiny. It is time to strike out, to change the game, to ensure accounting has an honorable presence in the academy.”
- “Don’t play the game. Redefine the game.”
What is Accounting Theory
Based on Liang (2010), “An Invitation to Theory”
What is theory?
“Theory is a coherent set of ideas that explains, or purports to explain, a set of real-world phenomena.”
- Coherence need not be at the surface level
“A theory offers a consistent, disciplined way to view the world, or a worldview”
Foundations
- Mathematics
- Bookkeeping
- Mathematical elegance of accounting structures
- Economics
- Neo-classical measurement
- Information economics and frictions
- Psychology
- Biases at the individual or organizational level
- Behavioral economics/finance
How does theory help guide empirics?
- Identifying research questions
- Economic research informs us of trade-offs
- Such trade-offs can suggest research questions
- Developing hypotheses
- Theory can predict direction and magnitude of effects
- Designing and conducting tests
- Theory can point to sources of endogeneity
- Interpreting findings
- Theory can provide testable predictions, and thus frame a discussion
- Theory can help organize thoughts/perspectives
Where are we at, revisited
- Measurement perspective
- Focus on valuation: How to [more accurately] measure something
- Relevant to practice
- Caveat: seemingly less likely to be academically relevant
- Information perspective
- Focus on identifying and providing information that is decision relevant
- Generally winning out over recent decades
- Caveat: “Information” provides a superstructure but lacks a solid foundation
- In contrast: Bookkeeping provides a solid foundation but no superstructure
Inferring bookkeeping activities
Arya, Fellingham and Schroeder (2000, IEA)
Overview
- Inverting Exercise
- Transactions \(\rightleftharpoons\) Financial statements
- Aggregation
- Information of economic activities
- Numbers under account balances
- Directed graph representation of the accounting system
- Characterization of all consistent transaction vectors
- Estimation Problem
- Picking the most likely transaction vector (based on priors and financial statements)
The inverting excercise
Seven transactions (accounting events)
- Purchase of raw materials inventory for cash
- Plant and administrative buildings acquired for cash
- Cash (period) expenses
- Cash sales
- Cost of goods sold
- Product cost depreciation
- Period cost depreciation
Balance Sheet
------ ------
Cash 2 10
Inventory 4 0
Net plant & buildings 6 0
Owners' Equity 12 10
Income Statement
------
Sales 10
Cost of goods sold 5
General and admin exp. 3
------
Income 2The directed graph representation of accounting system
Seven transactions (accounting events)
- Purchase of raw materials inventory for cash
- Plant and administrative buildings acquired for cash
- Cash (period) expenses
- Cash sales
- Cost of goods sold
- Product cost depreciation
- Period cost depreciation
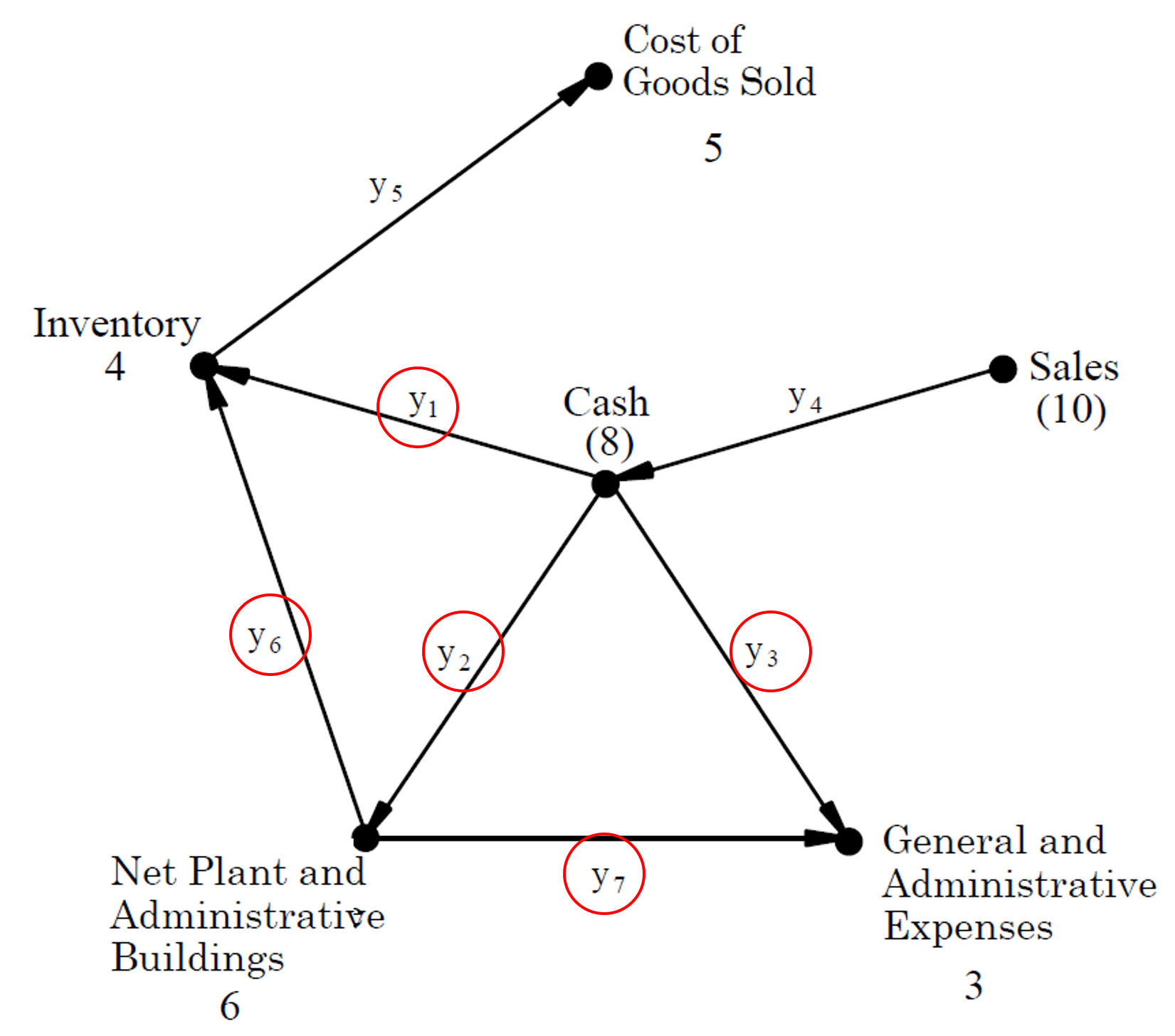
Characterization of all “consistent” transaction vectors
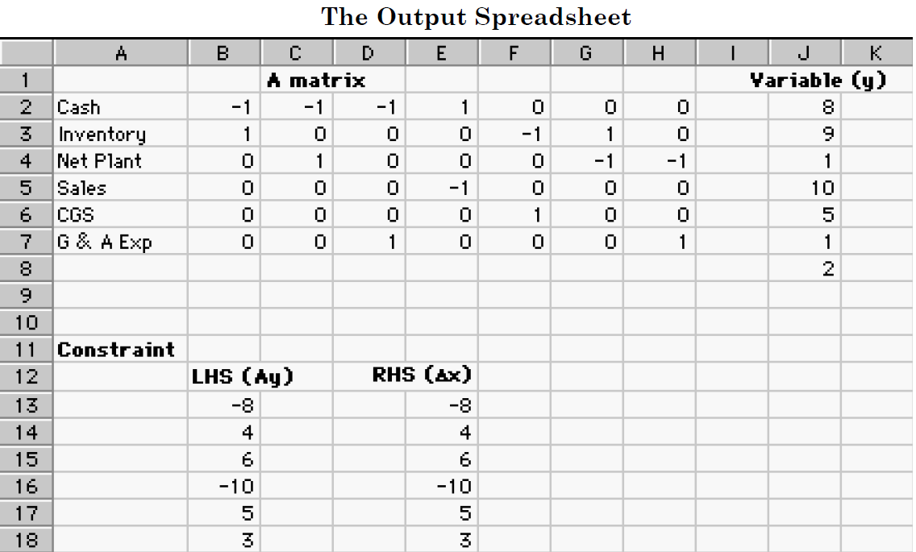

The estimation problem
\[ \begin{align*} &y=(I-P) y^p + P \bar{y}\\ &y\text{: the best guess} \begin{cases}\text{(1) consistent with $\Delta x$ and}\\\text{(2) most likely, i.e. the posterior mean}\end{cases} \\ &P\text{: projection matrix, } P=N(N^T N)^{-1} N^T\\ &\bar{y}\text{: the prior mean} \end{align*} \]
Two assumptions
1. The choice of which transactions to model
2. Transactions have identity variance-covariance structure
Inferring bookkeeping activities
Arya, Fellingham, Mittendorf and Schroeder (2004, CAR)
Understanding the directed graphs
- Source
- sets credit values
- Sink
- sets debit values
- Nodes
- Accounts
- \(\Delta\) for B/S
- level for I/S
- Accounts
- Edges
- Transaction classes
- flow
- Tracing out a path for consistency
Consistency
- Flow through starting with the max flow
- 7 in this case
- Flow through to sink
- If all flow from source is used and all flow through sink is used, then statement is consistent
- final flow from source and sink is the same
\(source=CR=DR=sink\)
- Easier to visualize as a flow of water
Application: Audit
- Run analysis on directed graph
- Issue: need to make the graph/possible transaction set first
- Can help to pinpoint where to look for problems
- Caveat: but only if the statements are not consistent
- Benefit: If not consistent, you have a good idea of where to look
Thoughts on Audit use
- Unlikely to detect intentional misreporting
- Such misreporting is largely in line with other transactions
- Could help with detecting transactions to the wrong accounts
- This can also be done by checking the journal entries…
Application: Ratio analysis
- Can determine bounds on ratios
- Caveat: no boundary if there is a negative loop
Example from the paper: Payables Turnover
- Typically substitute \(CGS + \Delta Inv\) for inventory purchases on credit
- \(\frac{CGS_t+\Delta Inv_t}{(A/P_{t-1}+A/P_t)/2}=\frac{2}{8.5}=0.24\)
- Adjusted: \(\frac{[0,2]}{8.5} = [0,0.24]\)
Discussion
Representations
- Are there any other sensible representations of double entry bookkeeping?
- What parts of the current system give rise to a directed graph?
- Accruals? Double entry?
Representations
Cash basis
Accrual basis additions
Aggregation
- How much aggregation is optimal? Tension between complexity and usefulness
- What about providing both aggregated and disaggregated information?
- What would an economy look like if only disaggregated information was made available?
Aggregation is central to these papers – without aggregation, we would already know the transactions.
Appendix
References
- Arya, Anil, John C. Fellingham, Jonathan C. Glover, Douglas A. Schroeder, and Gilbert Strang. “Inferring transactions from financial statements.” Contemporary Accounting Research 17, no. 3 (2000): 366-385.
- Arya, Anil, John C. Fellingham, and Douglas A. Schroeder. “Estimating transactions given balance sheets and an income statement.” Issues in Accounting Education 15, no. 3 (2000): 393-411.
- Demski, Joel S. “Is accounting an academic discipline?.” Accounting horizons 21, no. 2 (2007): 153-157.
- Demski, Joel S., John C. Fellingham, Yuji Ijiri, and Shyam Sunder. “Some thoughts on the intellectual foundations of accounting.” Accounting Horizons 16, no. 2 (2002): 157-168.
- Fellingham, John C. “Is accounting an academic discipline?.” Accounting horizons 21, no. 2 (2007): 159-163.
- Hatfield, Henry Rand. “An historical defense of bookkeeping.” Journal of Accountancy (pre-1986) 37, no. 000004 (1924): 241.
- Liang, Pierre Jinghong. “An invitation to theory.” China Journal of Accounting Research 3 (2010): 1-12.
- Liang, Pierre Jinghong. “Double-Entry Bookkeeping Appetizer.”
- Liang, Pierre Jinghong. “Appetizer One: MBA-classroom Use of an Accounting Structure.” Lecture, October 25, 2017.
- Littleton, A. C. “The evolution of the journal entry.” Accounting Review (1928): 383-396.
- Reynolds, Bernard. “Was Shakespeare an accountant?.” Journal of Accounting Research (1974): 367-371.
Packages used for these slides
- knitr
- revealjs
- visNetwork